Lotka Volterra Competition Model in Python - Part I

I have seen that exist many websites where Lotka-Volterra Predator-Prey model is explained detailed, and even with simulations in Python. However, it is less common to see sites explaining the Competition model. Then, I will try to make a very (very) simple explanation of this model as well as a simulation in Python (of course). You won't see much mathematical rigour (I am very sorry for that) as I intend to show this mainly to biologists.

Lotka-Volterra Competition model is the most famous mathematical approach of the interaction phenomenon of ecological competition. The generalised version of the model is defined as follows:

$\frac{dN_{i}}{dt} = r_{i}N_{i} (\frac{K_{i} - N_{i} - \sum_{j \neq i}^{n} \alpha_{ij}N_{j}}{K_{i}})  (1)$

Where:

$N$: Population size of i, j

$r$: Intrinsic growth rate of population i

$K$: Carrying capacity of population i

$\alpha_{ij}$: Competition effect of population j on population i

It could be a bit difficult to understand if you are not used to dealing with this kind of problems. We are going to simplify into a scenario where only two populations are competing, so we have now the following model:

$\frac{dN_{1}}{dt} = r_{1}N_{1}(1 - \frac{ [N_{1} + \alpha N_{2}]}{K_{1}}) (2)$

$\frac{dN_{2}}{dt} = r_{2}N_{2}(1 - \frac{[N_{2} + \beta N_{1}]}{K_{2}}) (3)$

For a biological context, we are going to assume that populations are always positive, so $N_{1}, N_{2} \in \mathbb{R}_{0}^{+}$. Also, we assume that populations will growth until a non-trivial carrying capacity, so $K_{1}, K_{2} \in \mathbb{R^{+}}$ and $r_{1}, r_{2} \in \mathbb{R^{+}}$. Finally, we are going to assume that competition between populations exist, then $\alpha, \beta \in \mathbb{R^{+}}$. Now, we can start our analysis.

Firstly, you have to understand is that the above equations are a system of ordinary differential equations. There is an extensive framework on this topic that I do not pretend to cover here, but if you are interested in this field, I recommend you to check this book:

Zill DG. (2013). A first course in differential equations with modelling applications. 10th edition. Brooks/Cole Cengage Learning. 384pp.

The system of differential equations in (2) and (3) represent how population size of competitors 1 and 2 changes over time. Both competitors have a logistic growth, but there is something else. If you focus on equation (2) you can see that the variable $N_{2}$ is present, so it means that the population size of competitor 1 will depend on the population size of competitor 2, and the other way around. Biologically that makes sense.

There exist three basic steps for analysing a system of ODEs:

1) Finding critical points. It consists of finding the conditions for which the system of ODEs remains constant. In other words, when the whole system of differential equations is equal to zero. Thus each equation must be equal to zero, for which we obtain the following conditions:

For equation (3)

$ \frac{dN_{1}}{dt} = r_{1}N_{1}(1 - \frac{ [N_{1} + \alpha N_{2}]}{K_{1}}) = 0 $

$ r_{1}N_{1}(1 - \frac{ [N_{1} + \alpha N_{2}]}{K_{1}}) = 0 $

$ r_{1}N_{1} = 0 $ or $ (1 - \frac{ [N_{1} + \alpha N_{2}]}{K_{1}}) = 0 $

$ N_{1} = 0 $ or $ K_{1} - N_{1} - \alpha N_{2} = 0 $

For equation (4)

$ \frac{dN_{2}}{dt} = r_{2}N_{2}(1 - \frac{[N_{2} + \beta N_{1}]}{K_{2}})  = 0 $

$ r_{2}N_{2} (1 - \frac{[N_{2} + \beta N_{1}]}{K_{2}})  = 0 $

$ r_{2}N_{2} = 0 $ or $ (1 - \frac{[N_{2} + \beta N_{1}]}{K_{2}})  = 0 $

$ N_{2} = 0 $ or $ K_{2} - N_{2} - \beta N_{1}  = 0 $

Using the above conditions, we can obtain the critical points of our system:

$P1 = (N_{1} = 0, N_{2} = 0) = (0, 0)$ Trivial

$P2 = (N_{1} = 0, K_{2} - N_{2} - \beta N_{1} = 0)$

$P2 = (0, K_{2} - N_{2} - \beta (0) = 0) = (0, K_{2} - N_{2} = 0)$

$P2 = (0, K_{2})$

$P3 = (K_{1} - N_{1} - \alpha N_{2} = 0, N_{2} = 0)$

$P3 = (K_{1} - N_{1} - \alpha (0) = 0) = (K_{1} - N_{1} = 0, 0) $

$P3 = (K_{1}, 0)$

$P4 = (K_{1} - N_{1} - \alpha N_{2} = 0, K_{2} - N_{2} - \beta N_{1} = 0)$

$P4 = (N_{1} = K_{1} - \alpha N_{2}, N_{2} = K_{2} - \beta N_{1})$

We need some extra arithmetic operation to obtain the P4

$N_{1} = K_{1} - \alpha [K_{2} - \beta N_{1}]$

$N_{1} = K_{1} - \alpha K_{2} + \alpha \beta N_{1}$

$N_{1} - \alpha \beta N_{1} = K_{1} - \alpha K_{2}$

$N_{1} (1 - \alpha \beta) = K_{1} - \alpha K_{2}$

$N_{1} = \frac{K_{1} - \alpha K_{2}}{1 - \alpha \beta}$

$N_{2} = K_{2} - \beta [K_{1} - \alpha N_{2}]$

$N_{2} = K_{2} - \beta K_{1} + \beta \alpha N_{2}$

$N_{2} - \beta \alpha N_{2} = K_{2} - \beta K_{1}$

$N_{2}(1 - \beta \alpha) = K_{2} - \beta K_{1}$

$N_{2} = \frac{K_{2} - \beta K_{1}}{1 - \beta \alpha}$

Thus, the critical points of the system are

$P1 = (0, 0)$ Trivial

$P2 = (K_{1}, 0)$ Competitor 1 survive, Competitor 2 is extinct

$P3 = (0, K_{2})$ Competitor 1 is extinct, Competitor 2 survive

$P4 = (\frac{K_{1} - \alpha K_{2}}{1 - \alpha \beta}, \frac{K_{2} - \beta K_{1}}{1 - \beta \alpha})$ Coexistence

At this point is a good idea to code. We are going to start by obtaining a solution to the model using arbitrary parameters and initial conditions. For example, I will simulate the model using:

Initial conditions: 

$N1_{0} = 6$

$N2_{0} = 5$

Parameters (arbitrary just for demonstration)

$r_{1} = 0.1$

$r_{1} = 0.1$

$\alpha = 0.4$

$\beta = 0.66$

$K_{1} = 100$

$K_{2} = 100$

Using this arbitrary initial condition and parameters, we obtain that the two species will coexist (i.e. both will reach stable non zero population in time) what is cool. However, it is even more interesting to determine the exact condition which determines the competitors coexist or one of them will get extinct. To do that, we will proceed to study the phase diagram.

2) Studying the Phase Diagram.

A phase diagram could be understood as a representation of the variables under study, the critical points and the trajectories of the solutions as vectors. This diagram also includes the nullclines of the system. Nullclines are trajectories where the derivate of a variable is equal to zero.

For example, for the Competitor $N_{1}$ the nullcline will be:

$N_{1} = 0$ a constante function (a line)

$K_{1} - N_{1} - \alpha N_{2} = 0$ a straight line

Analogously, the nullclines for Competitor $N_{2}$ will be:

$N_{2} = 0$ a constante function (a line)

$K_{2} - N_{2} - \beta N_{1} = 0$ a straight line

If we set up the X axis as $N_{1}$ and Y axis as $N_{2}$. Thus, the nullclines of Competitor $N_{1}$ would be a horizontal line ($N_{1}=0$) and a straight line ($K_{1} - N_{1} - \alpha N_{2} = 0$). Focusing in the latter we can determine where this line will cross the axes:

Making $N_{1} =0$, it follows:

$K_{1} - N_{1} - \alpha N_{2} = 0$

$K_{1} - 0 - \alpha N_{2} = 0$

$K_{1} =  \alpha N_{2}$

$N_{2} = \frac{K_{1}}{\alpha}$

Thus, when $N_{1} = 0$ the nullciline of competitor 1 will cut the $N_{2}$-axis in the value $N_{2} = \frac{K_{1}}{{\alpha}}$

Likewise, making $N_{2}=0$, it follows:

$K_{1} - N_{1} - \alpha N_{2} = 0$

$K_{1} - N_{1} - \alpha (0) = 0$

$N_{1} = K_{1}$

Thus, when $N_{2} = 0$ the nullcline of competitor 1 will cut the $N_{1}$-axis in the value $N_{1} = K$. Using these points we can define the straight line of the nullcline of competitor 1:

As you can see it is a straight line which cut the N_{1}-axis in $N_{1} = K = 100$ and the N_{2}-axis in the value $N_{2} = \frac{K_{1}}{{\alpha}} = 100/04 = 250$

Now, we must estimate the behaviour of the solution on the two regions separated for the nullcline. We can do a simple analysis for this:

If we only focus our attention in the $N_{1}$, we can see that $K_{1}$ marks the point where the nullcline divide the area in two regions (right and left). Thus, we can choose arbitrary values on each side of $K_{1}$.

- For instance, consider a value $N_{1}^{+} > K_{1}$. Replacing this value on (2), we can determine the derivate and then, the tendency of the solution:

$\frac{dN_{1}}{dt} = r_{1}N_{1}(1 - \frac{ [N_{1} + \alpha N_{2}]}{K_{1}})$

$\frac{dN_{1}^{+}}{dt} = r_{1}N_{1}^{+}(1 - \frac{ [N_{1}^{+} + \alpha N_{2}]}{K_{1}})$

As we are working on the $N_{1}-axis$, then $N_{2} = 0$

$\frac{dN_{1}^{+}}{dt} = r_{1}N_{1}^{+}(1 - \frac{ [N_{1}^{+} + \alpha (0)]}{K_{1}})$

$\frac{dN_{1}^{+}}{dt} = r_{1}N_{1}^{+}(1 - \frac{ N_{1}^{+}}{K_{1}})$

$\frac{dN_{1}^{+}}{dt} = r_{1}N_{1}^{+}(\frac{K_{1} - N_{1}^{+}}{K_{1}})$

We know that $r_{1}, K_{1},  N_{1}^{+} > 0$. Then:

$\frac{dN_{1}^{+}}{dt} =  (+) . (+) (\frac{K_{1} - N_{1}^{+}}{+})$

As $N_{1}^{+} > K_{1}$, it follows:

$\frac{dN_{1}^{+}}{dt} =  (+) . (+) (\frac{-}{+})$

$\frac{dN_{1}^{+}}{dt} =  (-)$

Thus, the derivate of the point N_{1}^{+} which is on the right side of the K_{1} will be negative, indicating the population will decrease. It can be represented as a vector pointing backwards. We can do a similar analysis to determine the behaviour on a point $N_{1}^{-} < K_{1}$, which is in the left side of the carrying capacity. The procedure will be similar:

$\frac{dN_{1}^{-}}{dt} =  (+) . (+) (\frac{K_{1} - N_{1}^{-}}{+})$

$\frac{dN_{1}^{-}}{dt} =  (+) . (+) (\frac{+}{+})$

$\frac{dN_{1}^{-}}{dt} =  (+)$

And here, the derivate is positive, which we can interpret that in this region population tend to increase. It can be represented as a vector pointing forward. This analysis can be replicated to all the points in the phase diagram, obtaining a vectorial field like this:

We can do an analogous analysis for the competitor $N_{2}$, obtaining a vectorial field like this:

But remember that these nullclines and victual fields are representations of each competitor in the absence of the another. However, in the competition model, we need to consider these figure simultaneously in the same figure. For the particular parameters and initial conditions we choose at the begging, we will obtain:

The above chart represents the Phase Diagram of the Competition model. The lime line indicate a particular solution for the initial conditions $N_{1}(0) = 6$, $N_{2}(0) = 5$. Pay attention to how all the vector point to a single point, which is not trivial. It means that under these combinations of values of parameters, all solutions always will end in the coexistence point. Precisely, it happens with our initial conditions $N_{1}(0) = 6$, $N_{2}(0) = 5$, look how the lime line ends up in the coexistence point, which values coincide with our simulations in the first figure of this post.

Continuing our analysis, you should realise the behaviour of the solutions in the phase diagram will depend on the combinations of parameters we use. If we vary the parameters we can obtain the classic predictions of the competition showed in many books of ecology:

Case 1:

$r_{1} = 0.1$

$r_{2} = 0.1$

$\alpha = 0.8$

$\beta = 1.2$

$K_{1} = 100$

$K_{2} = 100$

Case 2:

$r_{1} = 0.1$

$r_{2} = 0.1$

$\alpha = 1.3$

$\beta = 0.75$

$K_{1} = 100$

$K_{2} = 100$

Case 3:

$r_{1} = 0.1$

$r_{2} = 0.1$

$\alpha = 1.2$

$\beta = 1.3$

$K_{1} = 100$

$K_{2} = 100$

Case 4:

$r_{1} = 0.1$

$r_{2} = 0.1$

$\alpha = 0.8$

$\beta = 0.75$

$K_{1} = 100$

$K_{2} = 100$

We obtained nice figures, but what they mean? First of all, be aware that in all cases, the parameters are very similar; we are only changing the values of $\alpha$ and $\beta$. And you can see that changing these two parameters is enough to modify the qualitative behaviour of the system completely. Recalling the definition of $\alpha$ and $\beta$, they are:

$\alpha$ the effect of the competitor $N_{2}$ over N_{1}$

$\beta$ the effect of the competitor $N_{1}$ over N_{2}$

For the Case 1 ($\alpha = 0.8$, $\beta = 1.2$). We can see that $\beta > \alpha$, thereby the competitor $N_{1}$ have a major impact on competitor $N_{2}$ than $N_{2}$ over $N_{1}$. Biologically, it can be interpreted that $N_{1}$ is a better competitor than $N_{2}$. So, intuitively (thinking like an ecologist), you can conclude that $N_{1}$ will defeat $N_{2}$ in the ecological competition. And it is what happens in the respective figure (Figure Case 1). You can see that the vector (and the particular solution in lime) end up in $K_{1}$, meaning that under this conditions $N_{1}$ will reach its carrying capacity, and $N_{2}$ will be zero, which means that it will become extinct!

For the Case 2 ($\alpha = 1.3$, $\beta = 0.75$). We can see the opposite situation that Case 1. Here, $\beta > \alpha$ so the $N_{2}$ is the best competitor. Therefore, this population will reach its carrying capacity and $N_{1}$ will get extinct.

The Case 3 ($\alpha = 1.2$, $\beta = 1.3$) is more interesting. Here, both $N_{1}$ and $N_{2}$ are good competitors ($alpha$, $beta > 1$, it will be more clear in the next part), so will create it an unstable coexistence point; you can see it in the intersection of the nullclines. But, what population will win in the competitions? in this situation, both could win. What will determine the winner are the initial conditions (N_{1}(0), and N_{2}(0)). Once again, look at the vector, and you can see that depending on where you start the initial point, you can end in the $N_{1}$-axis or$ N_{2}$-axis. In the particular initial contusion we choose: $N_{1}(0) = 6$, and $N_{2}(0) = 5$, we can see that the $N_{1}$ is the winner and $N_{2}$ get extinct. But, what would had happened if we choose initial conditions like $N_{1}(0) = 20$, and $N_{2}(0) = 40$? You can see the vector would lead us to a situation where $N_{2}$ would be the winner and $N_{2}$ would get extinct.

 

Finally, the Case 4 ($\alpha = 0.8$, $\beta = 0.75$). Here, both $N_{1}$ and $N_{2}$ are bad competitor ($alpha$, $beta < 1$), and it is curios to note that this produce an stable equilibria in the intersection of the nullclines.

Now, some final points. Remember the equilibrium point of the system:

$P1 = (0, 0)$ Trivial

$P2 = (K_{1}, 0)$ Competitor 1 survive, Competitor 2 is extinct

$P3 = (0, K_{2})$ Competitor 1 is extinct, Competitor 2 survive

$P4 = (\frac{K_{1} - \alpha K_{2}}{1 - \alpha \beta}, \frac{K_{2} - \beta K_{1}}{1 - \beta \alpha})$ Coexistence

- P1, P2, and P3 are present in all Cases studied, but P4 only appear in Case 3 and 4.

- Vector never get closer to the P1, so P1 is a "repulsor" fixed-point. In contrast, vectors can go nearer ("attractors") the fixed-points P2, P3 and P4, or getaway of them ("repulsors"), which will depend on the parameters' values of $\alpha$ and $\beta$. We can determine exactly the conditions in which this fixed-points will be attractors or repulsors throughout a qualitative analysis of the system, and precisely it is what we do in the next part.

3) Determining the stability of the system.

As this post is becoming too long, I will develop this analysis in a future post. It will involve the analysis of the Jacobian matrix, so we will need to discuss some topics of linear algebra.

Automatisation of figures' creation using Python

Biologists, sometimes are involved in the preparation of field guides for species identification. Arranging many images could be an endless task. Because I am lazy, I always try to automatize the work.

Recently, I had to arrange 60 images in ten arrays of 2x3 (2 columns, three rows). Luckily, I found a code in Python that can do the work for me. The code was written for Evan Rosica, and it can be found here.

Herein, an example of how the code works!

We are going to merge the following images in a matrix of 2x2:

In #1 I am loading the libraries required. Basically, this code use "PIL."
In #2 you need to specify the directory where your images are stored (line 16).
In #3 the most relevant is that you should understand that all images will be resized according to the first image of your directory (line 28). However, you can change it quickly.
In #4 is a loop which will add each image in a sequence. There is not much mystery here.
In #5 I create some boxes and label for my images. I think it is possible to create a loop for this. If you can improve it you are welcome to try!
In #6 The final result is showed and saved if you want (uncomment line 84).

Below the full code

And here, the final result.

As you can see this code can help us to save time if we need to arrange too many images, even if you are writing papers that demand merging a lot of figures.

Categorize a Raster (DEM)

Although Raster files are visually attractive, they provide hard to interpret information because of is representing continuous data. So, they often are discretized in categories. There are many procedures to get it done (try QGis), but on this occasion, I will show how to do in R.

First, we need to load two libraries rgdal and raster, if you are using ess in emacs perhaps you must do some additional steps (you can email me). Now, we load our raster file, here, I'll use a Digital Elevation Model (DEM) of my country Peru (DEM_PERÚ.tif). You can download all the files in this link. However, this raster file doesn't match with the real form of my country, so we'll need to crop it, we'll do it later, but we are going to take advantage and load a vectorial shapefile which will be our mask (peru_disolved.shp). I recommend looking at the graphics to be sure that our files are loaded correctly.

 # 1. Packages  
 library(rgdal)          # Geospatial Data Abstraction Library  
 library(raster)          # Tools for gridded spatial data  
 # 2. Read DEM and convert to raster layer object  
 dem <- raster("~/Downloads/DEM_PERÚ.tif")     # raster  
 vperu <- readOGR("peru_disolved.shp", layer="peru_disolved")     # vectorial  
 plot(dem) # preliminar plotting  

Third, we are going to define the levels which will represent the categories. I have chosen only six levels (you can try others). We save the levels as a matrix. Fourth, using the function reclassify, we'll obtain a new file with the only the levels previously defined. Fifth, we obtain the graphic of the reclassified DEM.

 # 3. Generate a reclass matrix  
 m <- c(-Inf, 250, 1, 250, 500, 2, 500, 1000, 3, 1000, 2000, 4,  
     2000, 4500, 5, 4500, Inf, 6)     # specify dsired levels  
 rclmat <- matrix(m, ncol = 3, byrow = TRUE)  
 # 4. Reclassify the raster layer  
 reclassified_dem <- reclassify(dem, rclmat)  
 # 5. Plot the results  
 par(mfrow=c(1, 2))  
 plot(dem)  
 plot(reclassified_dem)  

The graphic is weird because we still need to crop it as a sixth step. You can quickly get it using the following code.

 # 6. Cropping  
 r1 <- crop(reclassified_dem, extent(vperu))  
 r2 <- mask(r1, vperu)  
 plot(r2)  

If you wish, you can save the files:

 # 7. Save new raster  
 writeRaster(reclassified_dem, "~/Downloads/reclassified_dem.tif", drivername="GTiff",  
       type = "Float32")  
 writeRaster(dem_crop, "~/Downloads/dem_crop.tif", drivername="GTiff",  
       type = "Float32")  

All the code is:

 # -*- coding: utf-8 -*-  
 # Author: Irbin B. Llanqui  
 #"""  
 # Language: R script  
 # This is a temporary script file.  
 #"""  
 # 1. Packages  
 library(rgdal)          # Geospatial Data Abstraction Library  
 library(raster)          # Tools for gridded spatial data  
 # 2. Read DEM and convert to raster layer object  
 dem <- raster("~/Downloads/DEM_PERÚ.tif")     # raster  
 vperu <- readOGR("peru_disolved.shp", layer="peru_disolved")     # vectorial  
 plot(dem) # preliminar plotting  
 # 3. Generate a reclass matrix  
 m <- c(-Inf, 250, 1, 250, 500, 2, 500, 1000, 3, 1000, 2000, 4,  
     2000, 4500, 5, 4500, Inf, 6)     # specify dsired levels  
 rclmat <- matrix(m, ncol = 3, byrow = TRUE)  
 # 4. Reclassify the raster layer  
 reclassified_dem <- reclassify(dem, rclmat)  
 # 5. Plot the results  
 par(mfrow=c(1, 2))  
 plot(dem)  
 plot(reclassified_dem)  
 # 6. Cropping  
 r1 <- crop(reclassified_dem, extent(vperu))  
 r2 <- mask(r1, vperu)  
 plot(r2)  
 # 7. Save new raster  
 writeRaster(reclassified_dem, "~/Downloads/reclassified_dem.tif", drivername="GTiff",  
       type = "Float32")  
 writeRaster(dem_crop, "~/Downloads/dem_crop.tif", drivername="GTiff",  
       type = "Float32")  

That's all for today.

A common error in adehabitatHR

Recently I figured out that in several forums people are asking about this error in the library adehabitatHR of R:

Error in getverticeshr.estUD(x[[i]], percent, ida = names(x)[i], unin,: The grid is too small to allow the estimation of home-range. You should rerun kernelUD with a larger extent parameter

Well, I'll try to explain this and solve it. First of all, this error occurs in the workflow to obtain polygons from a KDE volume, which is a common procedure in home range analysis.

In the first four steps of the following code, I simulate a dataset, which will represent the spatial position of two individuals.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

# -*- coding: utf-8 -*- # Author: Irbin B. Llanqui #""" # Language: R script # This is a temporary script file. #""" # 1. Packages library(adehabitatHR) # Package for spatal analysis # 2. Empty Dataframe points <- data.frame(ID = double()) XY_cor <- data.frame(X = double(), Y = double()) # 3. Assigning values (this will be our spatial coordinates) set.seed(17) for(i in c(1:100)){ if(i >= 50){points[i, 1] <- 1} else {points[i, 1] <- 2} XY_cor[i, 1] <- runif(1, 0, 100) XY_cor[i, 2] <- runif(1, 0, 100)} # 4. Transform to SpatialDataframe coordinates(points) <- XY_cor[, c("X", "Y")] class(points)

Now, I will estimate the kernel density using those spatial points.

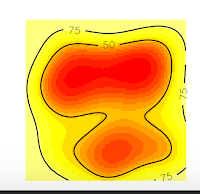
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

# 5. Domain x <- seq(0, 100, by=1.) # resolution is the pixel size you desire y <- seq(0, 100, by=1.) xy <- expand.grid(x=x,y=y) coordinates(xy) <- ~x+y gridded(xy) <- TRUE class(xy) # 6. Kernel Density kud_points <- kernelUD(points, h = "href", grid = xy) image(kud_points) # 7. Get the Volum vud_points <- getvolumeUD(kud_points) # 8. Get contour levels <- c(50, 75, 95) list <- vector(mode="list", length = 2) list[[1]] <- as.image.SpatialGridDataFrame(vud_points[[1]]) list[[2]] <- as.image.SpatialGridDataFrame(vud_points[[2]]) # 9. Plot par(mfrow = c(2, 1)) image(vud_points[[1]]) contour(list[[1]], add=TRUE, levels=levels) image(vud_points[[2]]) contour(list[[2]], add=TRUE, levels=levels)

And we obtain these nice plots. Now, we want to extract the contour lines at 75% of probability density. For that, we will use the function to get vertices as the following code:

 

1 2 3 4

# 10. Get vertices (Will be an Error) vkde_points <- getverticeshr(kud_points, percent = 75, unin = 'm', unout='m2') plot(vkde_points)

And we will get an ERROR!! Specifically, we will obtain the error I introduced at the beginning of this post.

Error in getverticeshr.estUD(x[[i]], percent, ida = names(x)[i], unin,: The grid is too small to allow the estimation of home-range. You should rerun kernelUD with a larger extent parameter

But why this happened? If you are a shrewd observer, you'll notice in the above plots that, the contour line at 75% is cut, and our domain doesn't include it. So, that is the reason for the error, is that R can't estimate the vertices of the contour line at 75% precisely because they are no in the domain, they were not computed. On the contrary, the contour line at 50% is entirely inside the domain, so if we ask for this vertices, we won't have any error.

1 2 3 4

# 10. Get vertices (Will be an Error) vkde_points <- getverticeshr(kud_points, percent = 50, unin = 'm', unout='m2') plot(vkde_points)

Now, if we want to extract 75% contour lines without an error, we only need to increase the grid in order to cover all the contour lines. In this case, I will increase the grid at 50 (see the item # 5. Domain x <- seq(-50, 150, by=1.) y <- seq(-50, 150, by=1.))

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

# 5. Domain x <- seq(-50, 150, by=1.) # resolution is the pixel size you desire y <- seq(-50, 150, by=1.) xy <- expand.grid(x=x,y=y) coordinates(xy) <- ~x+y gridded(xy) <- TRUE class(xy) # 6. Kernel Density kud_points <- kernelUD(points, h = "href", grid = xy) image(kud_points) # 7. Get the Volum vud_points <- getvolumeUD(kud_points) # 8. Get contour levels <- c(50, 75, 95) list <- vector(mode="list", length = 2) list[[1]] <- as.image.SpatialGridDataFrame(vud_points[[1]]) list[[2]] <- as.image.SpatialGridDataFrame(vud_points[[2]]) # 9. Plot par(mfrow = c(2, 1)) image(vud_points[[1]]) contour(list[[1]], add=TRUE, levels=levels) image(vud_points[[2]]) contour(list[[2]], add=TRUE, levels=levels) # 10. Get vertices (Will be an Error) vkde_points <- getverticeshr(kud_points, percent = 75, unin = 'm', unout='m2') plot(vkde_points)

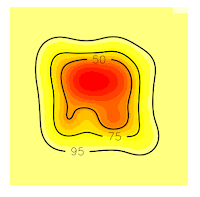
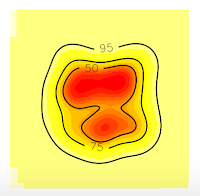
Now, all the contour lines are inside the grid, so we'll no see the error message. And that's all.

On species accumulation curves

On this occasion, I will share some quick tips related to the implementation of Species Accumulation Curves (SAC) using R (in the future I'll teach you how to do this in Python). First of all, we have to remember that SAC is a tool to assess and/or compare the alpha diversity. For instance, we can imagine someone who wants to know the alpha diversity (Species richness) in a particular place; for that, a sampling protocol is carried out. If we imagine this scenario, we can realize that while the sampling is performed the number of new species registered will decrease with respect the time. That is because, at the beginning of the sampling, the common species will be detected, but later, it will be harder to find new species because only remain the rares. This idea can be visualized in the form of the following curve (Moreno & Haffer, 2000):

As you can see, the curve increases rapidly with a few sampling units, but, as long as the sampling continues, the slope curve rises slower. When the increase of new species tend to zero (slope equal to zero or asymptote) it means that the inventory is complete. Thus, at this point, we would have reached the richness of the study area. In R, there are several ways to obtain accumulation curves through data; for example, we can use the "vegan" and "BiodiversityR" packages:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

# Dependences library("BiodiversityR") library("vegan") # Loading data data(BCI) # Using vegan package sp1 <- specaccum(BCI, method = "exact") sp2 <- specaccum(BCI, method = "random") # Using BiodiversityR package sp3 <- accumresult(BCI, method = "exact") sp4 <- accumresult(BCI, method = "random") # Comparing results using plots par(mfrow=c(1,2)) plot(sp1, col = "black", lwd = 3, xlab = "Samples", ylab = "Richness", main = "exact") plot(sp3, col = "red", xlab = "Samples", ylab = "Richness", add = TRUE) plot(sp2, col = "black", lwd = 3, xlab = "Samples", ylab = "Richness", main = "random") plot(sp4, col = "red", xlab = "Samples", ylab = "Richness", add = TRUE) legend("bottomright", c("vegan","BiodiversityR"), col = c("black","red"), lty = 1)

As you can see, vegan and BiodiversityR packages give similar results. The exact (Chiarucci et al. 2008) and random (Gotelli & Colwell 2001) indicate the accumulation functions used to obtain smoothed accumulation curve. Both packages have more tools to analyse diversity, particularly, in vegan is very easy using estimators to assess the completeness of the inventory: Chao, Jackknife 1, Jackknife 2, and Bootstrapping.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

# Dependences library("BiodiversityR") library("vegan") # Loading data data(BCI) # Using vegan package sp1 <- specaccum(BCI, method = "exact") sp2 <- specaccum(BCI, method = "random") # Using BiodiversityR package sp3 <- accumresult(BCI, method = "exact") sp4 <- accumresult(BCI, method = "random") # Comparing results using plots par(mfrow=c(1,2)) plot(sp1, col = "black", lwd = 3, xlab = "Samples", ylab = "Richness", main = "exact") plot(sp3, col = "red", xlab = "Samples", ylab = "Richness", add = TRUE) plot(sp2, col = "black", lwd = 3, xlab = "Samples", ylab = "Richness", main = "random") plot(sp4, col = "red", xlab = "Samples", ylab = "Richness", add = TRUE) legend("bottomright", c("vegan","BiodiversityR"), col = c("black","red"), lty = 1) # Estimators sp1_pool <- poolaccum(BCI, permutations = 1000) plot(sp1_pool)

The object created by "poolaccum" function gives you by default a figure using parameters of the "lattice" package:

But, it is not a very useful chart if we want to add the figure in a research presentation. For example, we likely wish to obtain just one plot without the frame, and all in black. Fortunately, we can modify the chart at our convenience. For example, Chao estimator is a great approach to assess the completeness of an inventory. So we want just this plot in an elegant way, whereby we need to delete the other sub-figures, remove some axes, box titles, change the colour, and so on. To do that, we can use the following code:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

# Dependences library("BiodiversityR") library("vegan") # Loading data data(BCI) # Using vegan package sp1 <- specaccum(BCI, method = "exact") sp2 <- specaccum(BCI, method = "random") # Using BiodiversityR package sp3 <- accumresult(BCI, method = "exact") sp4 <- accumresult(BCI, method = "random") # Comparing results using plots par(mfrow=c(1,2)) plot(sp1, col = "black", lwd = 3, xlab = "Samples", ylab = "Richness", main = "exact") plot(sp3, col = "red", xlab = "Samples", ylab = "Richness", add = TRUE) plot(sp2, col = "black", lwd = 3, xlab = "Samples", ylab = "Richness", main = "random") plot(sp4, col = "red", xlab = "Samples", ylab = "Richness", add = TRUE) legend("bottomright", c("vegan","BiodiversityR"), col = c("black","red"), lty = 1) # Estimators sp1_pool <- poolaccum(BCI, permutations = 1000) plot(sp1_pool) # Plot manipulating lattice plot(sp1_pool, display = "chao", col = "black", auto.key = FALSE, grid = F, strip = FALSE, xlab = "Sample", par.settings = list(axis.line = list(col = 0)), scales = list(col=1, tck=c(1,0)), panel = function(...){ lims <- current.panel.limits() panel.xyplot(...) panel.abline(h=lims$ylim[1], v=lims$xlim[1]) })

Done!, we have made an accumulation curve with 95% confidence intervals (CI). The chart shows us that the inventory is still incomplete because the CI of the Chao estimator is not stable. In the following figure, we can see how adding more sampling units make the Chao estimator stable. Therefore, in this case, we can conclude that the inventory is complete. The final richness or number of species is equal to the value of the asymptote of the Chao estimator.

REFERENCES

Chiarucci, A., Bacaro, G., Rocchini, D., & Fattorini, L. (2008). Discovering and rediscovering the sample-based rarefaction formula in the ecological literature. Community Ecology, 9(1), 121–123. http://doi.org/10.1556/ComEc.9.2008.1.14

Gotelli, N. J., & Colwell, R. K. (2001). Quantifying biodiversity: Procedures and pitfalls in the measurement and comparison of species richness. Ecology Letters, 4(4), 379–391. http://doi.org/10.1046/j.1461-0248.2001.00230.x

Moreno, C. E., & Halffter, G. (2000). Assessing the completeness of bat biodiversity inventories using species accumulation curves. Journal of Applied Ecology, 37(1), 149–158. http://doi.org/10.1046/j.1365-2664.2000.00483.x

Projecting coordinates in Python

Sometimes we have to manipulate huge spatial databases, and it uses to be a headache if we must to convert the spatial point to a different projection. Well, an excellent way to solve this sort of issues is taking advantage of the libraries of python. In this case, I am going to describe how to use the package utm for it.

First, we are going to simulate some spatial data in a decimal projection.

1 2 3 4 5 6 7 8 9 10 11 12 13 14

import matplotlib.pyplot as plt import numpy as np import pandas as pd import utm lat = np.linspace(20, 40, 100) long = np.linspace(60, 70, 100) index = np.arange(1,101) d = {'x': pd.Series(lat, index=index), 'y': pd.Series(long, index=index)} df = pd.DataFrame(d) print(df)

Done!, we have already created a Dataframe with one hundred of spatial points in decimal degrees. Now, we are going to project them to UTM. First, we make a temporal "temp" variable which will store our projected XY coordinates. Afterwards, we are going to use the function utm.from_latlon() in a loop. This instruction will put each project coordinate in your variable "temp" that you created recently.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

import matplotlib.pyplot as plt import numpy as np import pandas as pd import utm lat = np.linspace(20, 40, 100) long = np.linspace(60, 70, 100) index = np.arange(1,101) d = {'x': pd.Series(lat, index=index), 'y': pd.Series(long, index=index)} df = pd.DataFrame(d) #print(df) temp = [[None]*1 for ii in range(len(df.x))] ## Use the utm package to transform coordinates for i in np.arange(0, len(df.x)): temp[i] = utm.from_latlon(df.y[i+1], df.x[i+1]) # Transform in a dataframe data = pd.DataFrame(temp) data.columns = ['X', 'Y', 'Zone', 'Code'] print(data)

Finally, we convert the projected data to a DataFrame and assign this to a new variable "data", and that's all. This procedure helps me to transform a database with two hundred thousand locations, so it is useful to project massive databases.

Diffusion equation

The diffusion equation is widely discussed in the literature, especially in physics and mathematics. However, the diffusion equation also has relevance in other fields, for instance, biology, where it can be useful to understand some biological phenomena at different scales, including population biology. Therefore, it is crucial to know how to solve it.

The diffusion equation is a partial differential equation which involves both a time and space. In 1D it would be:

$\frac{\partial u}{\partial t} = D \frac{\partial^2 u}{\partial x^2}$

It can be discretised using numerical methods. In this case, we are going to use the finite difference method, so that the above equation can be discretised as follows:

$\frac{u^{t+1}_{i} - u^{t+1}_{i}}{\Delta t} = D \frac{u^t_{i+1} - 2u^t_{i} + u^t_{i-1}}{\Delta^2x}$

where, $t$ indicate the time set and $i$ the x position.

To obtain the steady-state, we are going to programming this in python. The below code solve the diffusion equation numerically

import numpy as np
import matplotlib.pyplot as plt

#Setting parameters
nx = 101
dx = 0.01
nt = 20000
D = .1
dt = 0.0001 #be aware setting this value

#Initial conditions
u = np.zeros(nx)
u[25:75] = 2
un = u.copy()

#Numerical scheme: Finite differences
for n in range(nt):
    for i in range(1, nx-1):
        un = u.copy()
        u[i] = un[i] + D * dt /dx**2* (un[i+1]-2*un[i]+un[i-1])

#Plot the results
plt.plot(np.linspace(0, 1, 101), u)
plt.ylim(0, 4)
plt.xlim(0, 1.)
plt.show()

The solution is

Where it is shown how the distribution diffuses across the domain; however, as time passes, the distribution density tends to zero, so that the mass conservative property is not satisfied. If we wish to maintain a constant mass, we have to apply boundary conditions, in this case, we need to set-up a zero flux condition in the extremes of the domain. Then:

$\frac{\partial u}{ \partial t} = 0 $

import numpy as np
import matplotlib.pyplot as plt

#Setting parameters
nx = 101
dx = 0.01
nt = 20000
D = .1
dt = 0.0001 #be aware setting this value

#Initial conditions
u = np.zeros(nx)
u[25:75] = 2
un = u.copy()

#Numerical scheme: Finite differences
for n in range(nt):
    for i in range(1, nx-1):
        un = u.copy()
        u[i] = un[i] + D * dt /dx**2* (un[i+1]-2*un[i]+un[i-1])                                                                                                       # Zero flux condition
        u[0] = u[1]
        u[-1]= u[-2]                                                            
#Plot the results
plt.plot(np.linspace(0, 1, 101), u)
plt.ylim(0, 4)
plt.xlim(0, 1.)
plt.show()

Here, zero flux condition is included straightforward by adding:  u[0] = u[1]   (left)  and
u[-1]= u[-2] (right). Then, the mass can not go outside of the domain.

But!, be careful, because this zero flux condition only works for this simple equation. If you are working with different models, for instance, the advection-diffusion equation, zero flux condition has to be implemented differently.